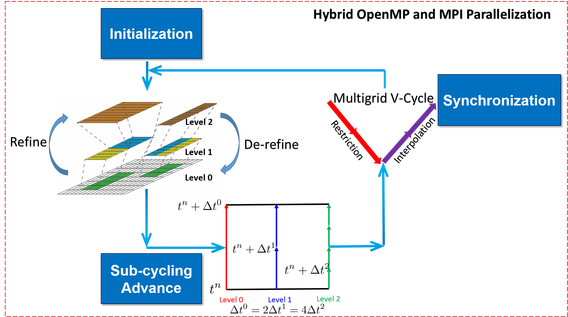
The Adaptive Mesh Refinement (AMR) technique provides a powerful tool for high-fidelity, high-resolution simulations. To capture complex processes in simulations, a high grid resolution is needed to resolve small structures. However, these fine structures may not be present everywhere, therefore one does not need or maybe cannot afford a fine grid of uniformly high resolution across the whole domain. The need to resolve local fine features can be addressed by the AMR method, which increases the grid resolution in regions of interest as needed during the simulation while leaving general estimates in other regions.
Based on AMReX, we have developed a block-structured AMR (BSAMR) framework on the multi-level collocated grid. This framework utilizes the level set (LS) method for simulating two-phase flows and the distributed Lagrange multiplier method for fluid-structure interaction (FSI) problems. Both the subcycling and non-subcycling methods are implemented for time advancement in this unified framework. We have used AMR to simulate a wide range of fluid mechanics problems, including the dam breaking, wave energy converters, and biomimetics.
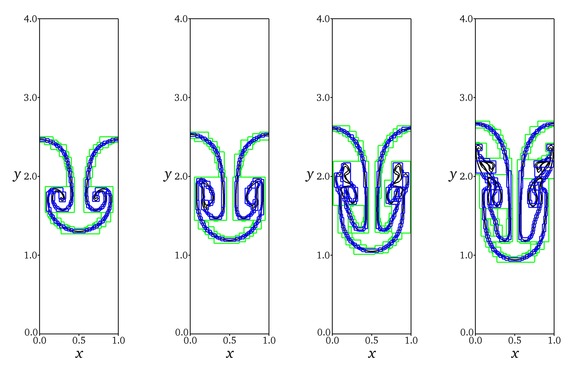
The black line represents the air-water interface. The green and blue lines represent the patches on level 1 and level 2, respectively.
Selected Publications:
- Zeng, Y., Liu, H., Gao, Q., Almgren, A., Bhalla, A. & Shen, L. (2023), “A consistent adaptive level set framework for incompressible two-phase flows with high density ratios and high Reynolds numbers,” Journal of Computational Physics, Vol. 478, 111971.
- Zeng, Y., Bhalla, A. & Shen, L. (2022), “A subcycling/non-subcycling time advancement scheme-based DLM immersed boundary method framework for solving single and multiphase fluid-structure interaction problems on dynamically adaptive grids,” Computers and Fluids, Vol. 238, 105358.
- Zeng, Y., Xuan, A., Blaschke, J. & Shen, L. (2022), “A parallel cell-centered adaptive level set framework for efficient simulation of two-phase flows with subcycling and non-subcycling,” Journal of Computational Physics, Vol. 448, 110740.